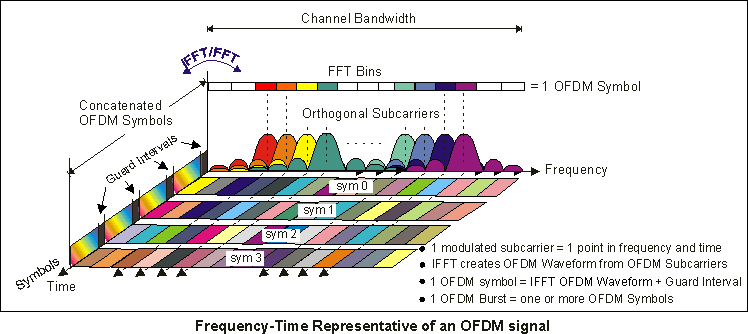
引言

在当今的无线通信技术中，从Wi-Fi到5G，从广播电视到卫星通信，OFDM作为一种高效的调制技术得到了广泛的应用。相比传统的单载波传输，OFDM通过将数据分割到多个正交子载波上传输，不仅能够显著提高带宽利用率，还能有效应对多路径干扰等无线信道问题。

OFDM的魅力在于它简单却强大的核心思想：将一个复杂的高速信号“分而治之”，分成多个低速子信号进行并行传输。这种方式既解决了码间干扰（ISI）的困扰，同时能够高效适应不同的传输环境，为高速稳定的数据传输提供支持。

本文将从一些基础性的东西出发，逐步解析OFDM的整体流程。

1. 载波与信息

信号是用来传递信息的工具。它可以是模拟信号（如声音、视频）或数字信号（如0和1组成的二进制代码）。信号本身往往处于低频或基带状态，在这种状态下，它无法有效传播到远距离。例如无线通信中，天线的尺寸往往和信号的波长成比例，而波长$ \lambda = \frac{c}{f} $ （其中$f$是频率，$c$是光速），这就意味着低频信号的波长非常长，需要极大尺寸的天线，在实际应用中存在巨大的困难。

载波是一种较高频率的周期性波形，它本身是没有信息的，但可以通过调制改变其属性（如幅度、频率或相位），从而“携带”信号进行传输。载波的高频特性使得信号能以更高效的方式传播到远距离，同时方便利用频谱资源和区分不同信道。

简单来说，信号是内容，载波是运输工具，调制是将信号映射在载波的一种方式，用以实现无损的信息传递。

这里使用数字调制来解释，假设有比特流00，01，10，11，我们就可以用一个幅度表示两个比特，四个幅度表示这八个比特。我们用简化过的公式来表示这个信号

$$s(t) = A\cdot cos(2\pi f_c t)$$

其中$A$就是我们要发送的信号映射的幅度，$cos(2\pi f_c t)$ 是我们的载波。如果我们将00，01，10，11映射在1，2，3，4这四个幅度上，依次发送，那么波形应该如以下图像所示：

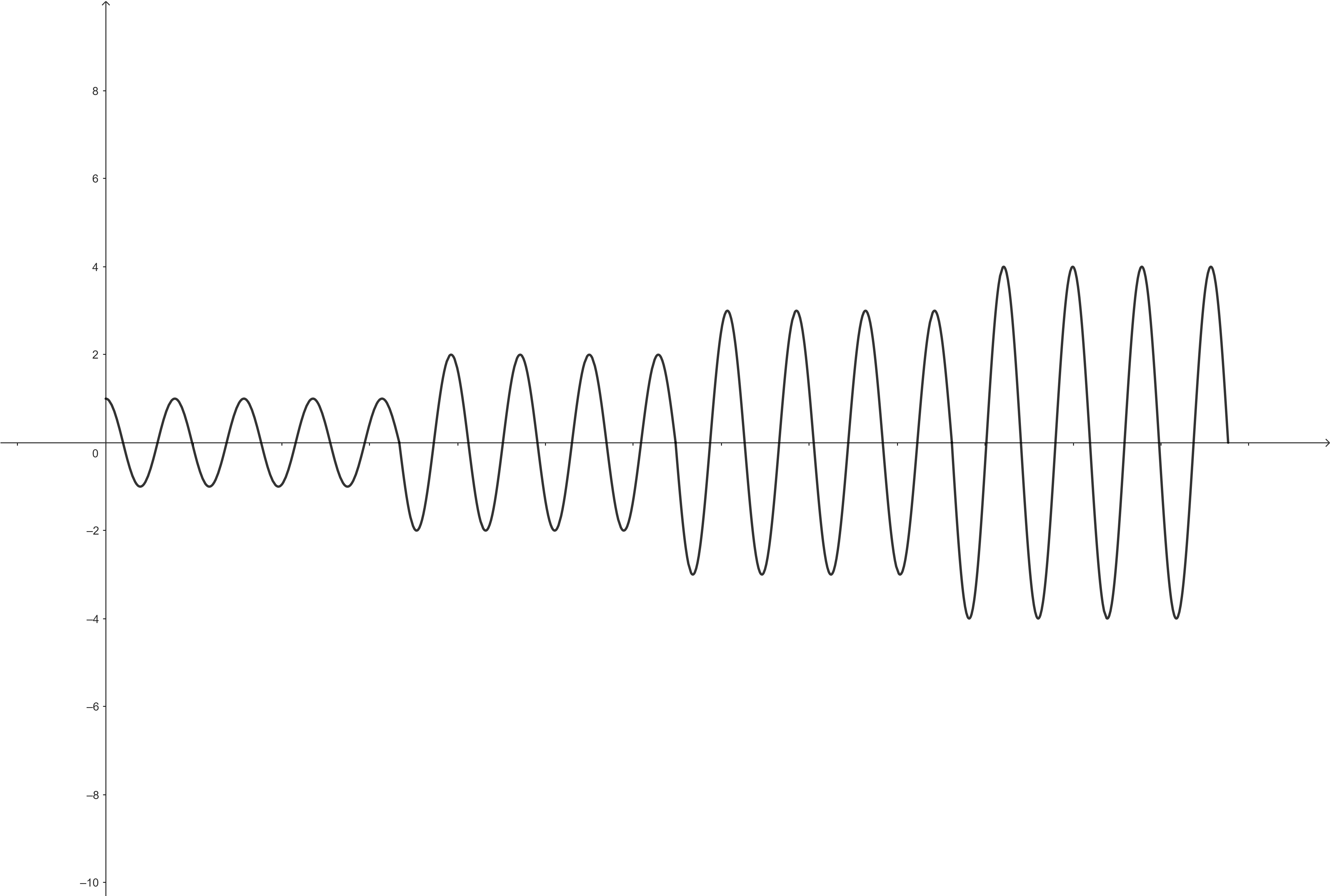
这就是一个简化过的典型的4-ASK（四阶幅度键控，4-Amplitude Shift Keying），通过在载波的幅度上附加信息以实现通过载波传送信息。传统幅度调制通过改变载波的幅度传递信息，但其本质是单一维度的调制——所有信息都编码在幅度这一个自由度上。

2. 正交性

这时候我们可以引出一个概念：正交性

两个载波$\phi_1(t)$和$\phi_2(t)$在符号周期$T$内满足正交条件：

$$\int\limits_{0}^{T}\phi_1(t)\cdot\phi_2(t)dt = 0$$

如果我们让$\phi_1(t) = sin(2\pi f_c t)$，$\phi_2(t) = cos(2\pi f_c t)$，通过简单的计算可以知道，这两个载波是正交的。

这意味着我们如果有一个信号$s(t) = A\cdot\phi_1(t) + B\cdot\phi_2(t)$，也就是两个载波的叠加，从发送端发送，从接收端接收到后，可以同过正交性的原理重新剥离出两个信号：

$$A = \int\limits_{0}^{T}s(t)\cdot\sin(2\pi f_c t)dt $$

$$B = \int\limits_{0}^{T}s(t)\cdot\cos(2\pi f_c t)dt $$

这样我们就可以实现在一个频段下同时传输两个独立的载波，两个载波互不干扰且能完美的分离出来。

3. I/Q调制

在通信系统中，正交性为高效频谱利用提供了理论可能，但要将这种数学特性转化为实际技术，需要一种能将两路独立信号嵌入同一频段的调制方法——IQ调制（In-phase/Quadrature Modulation）。

传统调制技术（如AM或FM）仅利用单一维度传输信息，例如通过幅度或频率变化编码数据，这导致频谱效率低下、抗干扰能力弱，且难以扩展。例如，若想通过调幅传输4比特数据，需要定义16种不同的幅度等级，但噪声稍大便会导致幅度失真，误码率急剧上升；而若叠加多载波提升容量，硬件成本和功耗又会失控。正交性的出现打破了这一僵局：通过使用相位差90度的两个载波（如$cos(2\pi f_c t)$和$sin(2\pi f_c t)$），可以在同一频段内并行传输两路独立信号，互不干扰。

IQ调制将这一理论付诸实践——它将数据拆分为同相分量（I路）和正交分量（Q路），分别调制到两个正交载波上，再合成为单一信号：

$$s(t) = I(t)cos(2\pi f_c t) – Q(t)sin(2\pi f_c t)$$

接收端通过正交解调，可精确分离出I和Q信号。这种设计不仅将频谱效率直接翻倍（从单边带的50%利用率提升至双边带100%），而传统单维度调制需复杂的反馈电路。更重要的是，IQ调制为高阶调制技术铺平了道路——通过在I/Q平面上灵活布置星座点，其中，I/Q平面是一个复平面。

4. QAM （Quadrature Amplitude Modulation）正交幅度调制

I/Q调制中其中一个很重要的方法就是QAM（Quadrature Amplitude Modulation）正交幅度调制。QAM本质上是IQ调制的具体应用。

在QAM中，数据被分配到I和Q通道，分别对这两个分量的幅度进行调制（而非相位或频率），从而实现幅相联合调制。I和Q的幅度组合对应星座图中的不同符号。

我们可以直接把信息映射到二维的复平面上（I-Q坐标系），每个QAM符号由两个独立的幅度$I$和$Q$定义：

$$s(t) = I\cdot cos(2\pi f_c t) \ – \ Q\cdot \sin(2\pi f_c t)$$

$$s(t) = Re{(I(t) + jQ(t)) \cdot e^{j2\pi f_c t}}$$

以4QAM举个例子，通过在星座图（二维复平面）中的四个点传递信息，其中每个点是一个符号，映射2比特的信息。

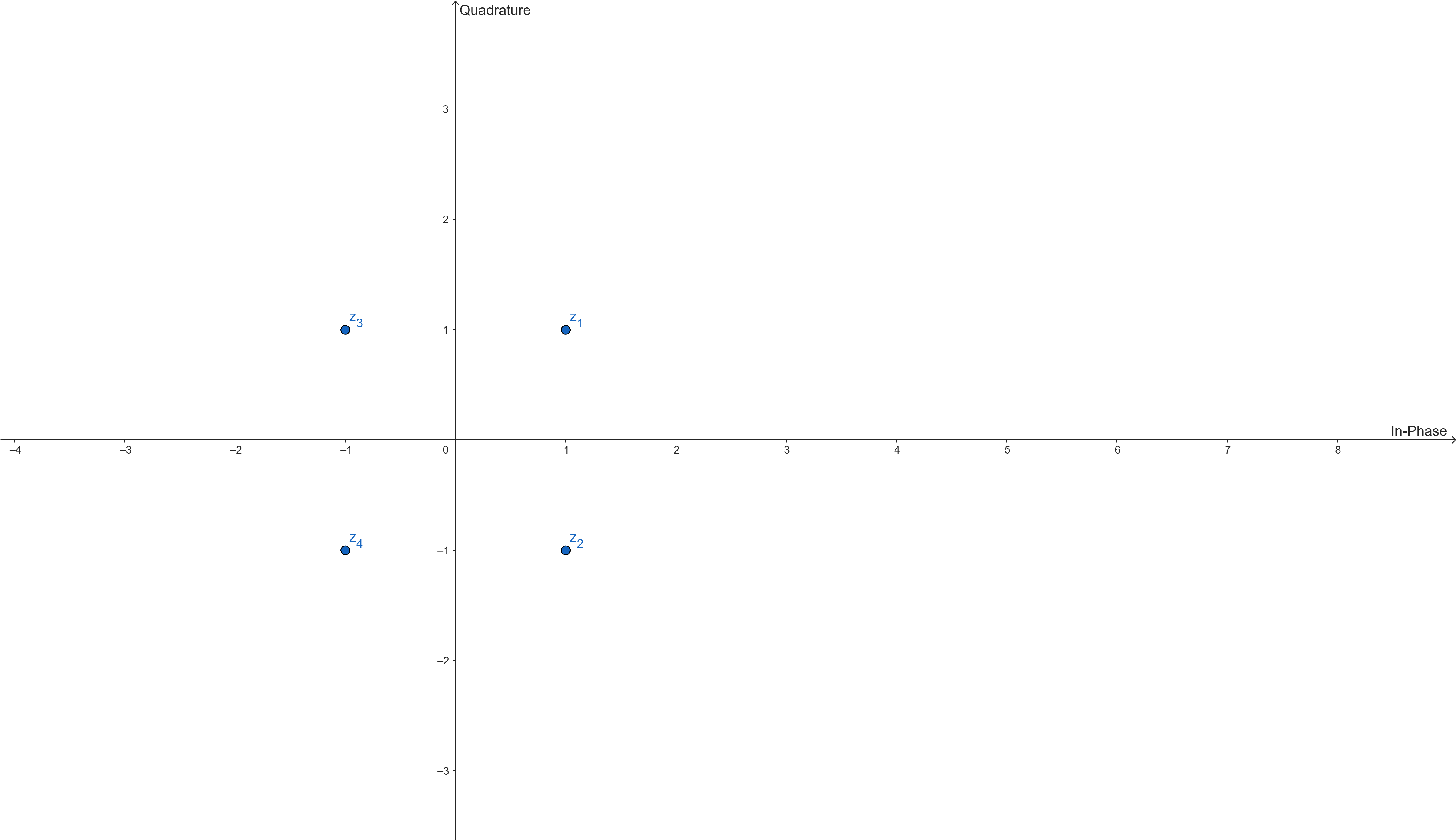
我们可以把00，01，11，10映射到四个点$z_1$，$z_3$，$z_4$，$z_2$上，我们可以用复数表示为：$1+i$，$-1+i$，$-1-i$，$1-i$。如果从我们的信号的公式来看，就可以得知：

$$s_{Rz1}(t) = cos(2\pi f_c t) \ – \ \sin(2\pi f_c t)$$

$$s_{Rz2}(t) = cos(2\pi f_c t) + \sin(2\pi f_c t)$$

$$s_{Rz3}(t) = – \ cos(2\pi f_c t) \ – \ \sin(2\pi f_c t)$$

$$s_{Rz4}(t) = – \ cos(2\pi f_c t) + \sin(2\pi f_c t)$$

这就是四个符号的QAM信号，依次发送即可。

5. OFDM （Orthogonal Frequency Division Multiplexing）正交频分复用技术

尽管QAM在理想信道中能实现高频谱效率，但在宽带多径信道中面临以下问题：

符号间干扰（ISI, Inter-Symbol Interference）：高速传输时，符号周期（T）缩短，多径时延扩展可能超过T，导致相邻符号在时域重叠，接收端难以区分。尤其是当时延超过符号周期的时候，这种难以区分的情况就很严重。

复杂均衡需求：单载波QAM需要高阶时域均衡器（如判决反馈均衡器DFE）来消除ISI，但计算复杂度随带宽指数增长。

频率选择性衰落：宽带信道不同频段的衰落差异显著，导致部分子载波深度衰落，整体性能受限。

而OFDM基本上做的最重要的两件事情就是将多个符号时间为$1/T_s$QAM符号直接转换为$\frac{N}{T_s}$时域的OFDM符号，也就是说延长了符号周期时间，并且直接生成时域信号。

而生成时域信号最重要的方法就是IFFT。

在OFDM系统中，逆快速傅里叶变换（IFFT） 用于将频域符号转换为时域信号。其数学公式基于离散傅里叶逆变换（IDFT），定义如下：

$$x[n] = \frac{1}{N} \sum_{k = 0}^{N – 1} X[k] \cdot e^{j2\pi kn/N}$$

其中：

• $X[k]$：频域中第 k 个子载波的复数符号（例如QAM符号）。
• $x[n]$：时域信号的第 n 个采样点。
• $N$：子载波总数。

IFFT有着极佳的计算性能，硬件实现的复杂度也较低。

而IFFT输出的就是复数序列，假设一个QAM信号的符号时间是$1/T_s$，有N个OFDM子载波，那么一个OFDM的符号有N个复数，且总符号时间为$\frac{N}{T_s}$。这就避免了符号周期过短导致的接收端难以区分。

另一个OFDM重要的步骤就是CP（Cyclic Prefix）

在无线通信中，信号会通过不同的路径（例如直接路径和反射路径）到达接收端，这种现象称为多径效应。由于路径长度的差异，不同路径的信号到达时间会有延迟，导致符号间干扰（ISI，Inter-Symbol Interference）。在OFDM中，如果前一个符号的信号延迟扩展到下一个符号的接收时间内，就会破坏子载波的正交性，进而影响接收端正确解调数据。

为了解决多径效应带来的ISI问题，OFDM引入了循环前缀，在发送端，将每个OFDM符号的末尾部分数据复制到符号的前面，形成一个前缀。这个前缀就是“循环前缀”，因为它是从符号尾部循环取出的。CP的长度通常要大于信道的最大时延扩展（即多径效应的最长延迟），这样可以确保多径分量不会干扰到下一个符号的有效数据部分。CP被加到每个OFDM符号的开头，构成一个完整的传输符号：CP + 数据部分。

在接收端，由于多径效应，接收到的信号是多个延迟版本的叠加。有了CP，即使存在时延扩展，接收端只需丢弃CP部分（因为它吸收了多径干扰），然后从有效数据部分开始采样。这样，前一个符号的多径分量就不会影响到当前符号的有效数据，避免了ISI。

通过信道后，FFT后再解调QAM，就能得到我们的数据流了。