引言

正交幅度调制（QAM）作为现代数字通信的核心技术，通过幅度和相位联合调制实现了高频谱效率传输。从Wi-Fi到5G，从光纤通信到卫星链路，QAM技术始终扮演着关键角色。误码率（BER）作为衡量通信系统可靠性的核心指标，其理论计算方法对系统设计具有重要指导意义。本文将系统性推导4QAM、16QAM的BER表达式。

4-QAM

1. 信号能量

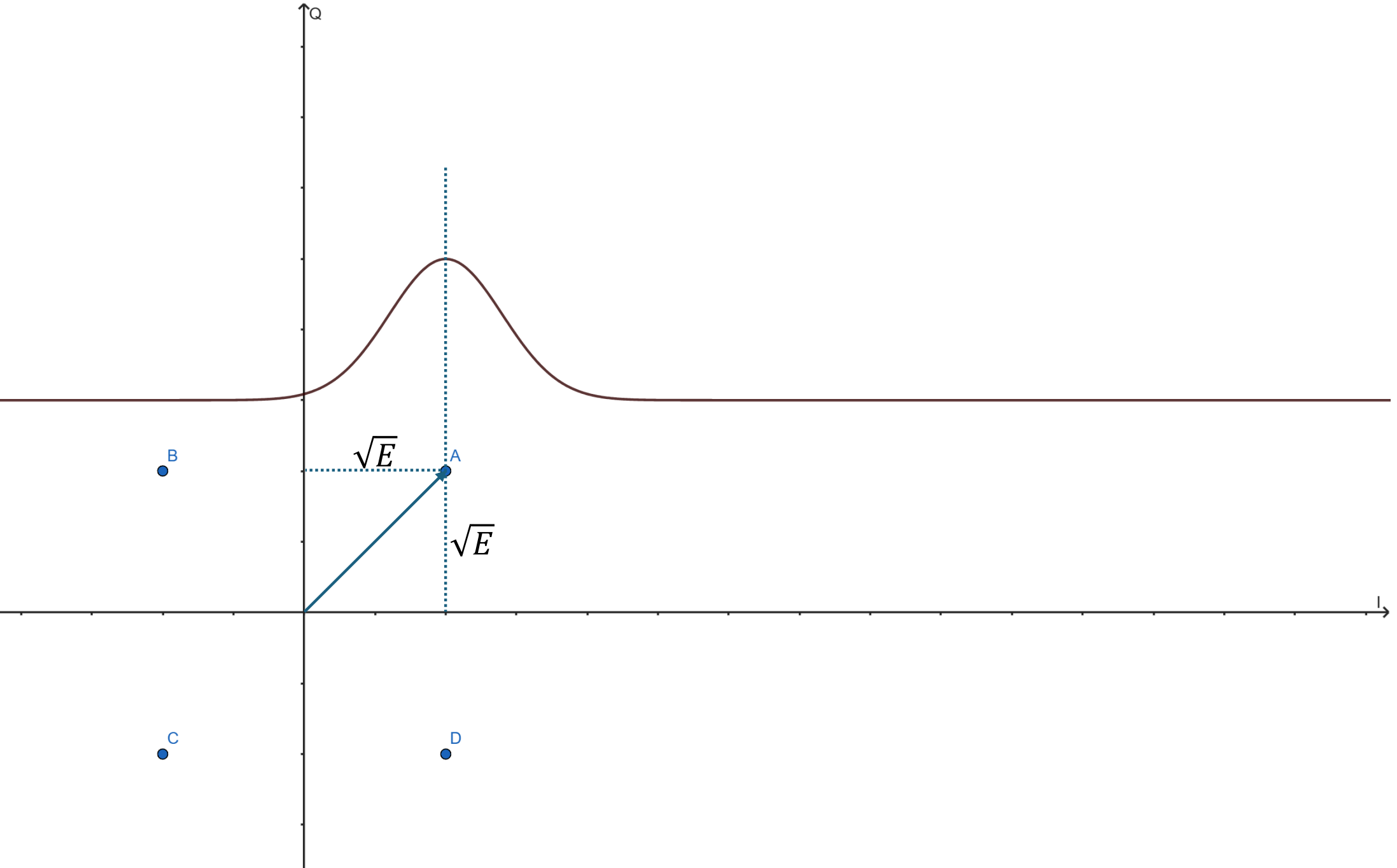
在一个4-QAM的星座图中，以A点举例。

$$S_A = \sqrt{E} + j\sqrt{E}$$

$$E_{s} = (\sqrt{E})^2 + (\sqrt{E})^2 = 2E$$

其中，$\sqrt{E}$是$I$和$Q$两个维度的各自的幅度，$E$是每个维度的能量，每个符号在两个幅度上的能量之和是$2E$。

因为是4-QAM，每个符号携带的比特数为 $log_{2}(M) = 2$，因此：

$$E_b = \frac{E_s}{log_{2}(M)} = \frac{E_s}{2} = E$$

2. AWGN信道

在AWGN信道中，接受到的信号$r$可以表示为：

$$r = s + n$$

其中$s$是发送的信号，$n$是噪声，为复高斯随机变量，其实部$n_I$相互独立$n_Q$，每个正交的分量都服从均值为0，方差$\sigma^2 = \frac{N_0}{2}$的分布，其中整个复信号的方差为$N_0$。

3. 裁决

在接收端，采用最小距离裁决规则，即选择与接收信号$r$，也就是A点，欧氏距离最小的符号点。由于4-QAM符号点是对称的，判决区域可以用坐标轴划分：

• $I$分量：如果$r_I > 0$，判定$s_I = \sqrt{E}$，否则$s_I = -\sqrt{E}$。
• $Q$分量：如果$r_Q > 0$，判定$s_Q = \sqrt{E}$，否则$s_Q = -\sqrt{E}$。

$I$和$Q$的裁决是相互独立的。

4. 计算BER

噪声$n_I$和$n_Q$服从高斯分布：

$$n_I \sim \mathcal N (0, \frac{N_0}{2}) , n_Q \sim \mathcal N (0, \frac{N_0}{2})$$

$$Q(x) = \frac{1}{\sqrt{2 \pi}} \int_{x}^{\infty} e^{- \frac{t^2}{2}}dt$$

对于随机变量$X \sim \mathcal N (\mu , \sigma^2)$，有：

$$P(X < a) = Q(\frac{\mu – a}{\sigma})$$

$$P(X > a) = Q(\frac{a – \mu}{\sigma})$$

以A点举例，$s = (\sqrt{E}, \sqrt{E})$，在接收端，从I分量的角度，计算A落在错误的区域$r_I<0$的概率：

$$r = \sqrt{E} + n_I$$

$$P(r_I < 0) = P(\sqrt{E} + n_I <0) = P(n_I < – \sqrt{E}) = Q(\frac{\sqrt{E}}{\sigma})$$

则落在I分量上正确的概率为$1 – Q(\frac{\sqrt{E}}{\sigma}) $，同时在两个分量上正确的概率为：

$$[1 \quad – \quad Q(\frac{\sqrt{E}}{\sigma})]^2 $$

在两个分量上出错的概率为：

$$P_{ser} = 1 – [1 – Q(\frac{\sqrt{E}}{\sigma})]^2 = 2Q(\frac{\sqrt{E}}{\sigma})\quad – \quad Q(\frac{\sqrt{E}}{\sigma})^2 = 2Q(\sqrt{\frac{E_s}{N_0}})\quad – \quad Q(\sqrt{\frac{E_s}{N_0}})^2$$

当$\frac{E_b}{N_0} \gg 1$时，可以忽略掉$Q(\sqrt{\frac{2E_b}{N_0}})^2$：

$$P_{ser} \approx 2Q(\sqrt{\frac{E_s}{N_0}})$$

$$BER \approx \frac{P_{ser}}{Bits \quad per \quad Symbol} = Q(\sqrt{\frac{E_s}{N_0}}) = Q(\sqrt{\frac{2E_b}{N_0}})$$

16-QAM

1. 信号能量

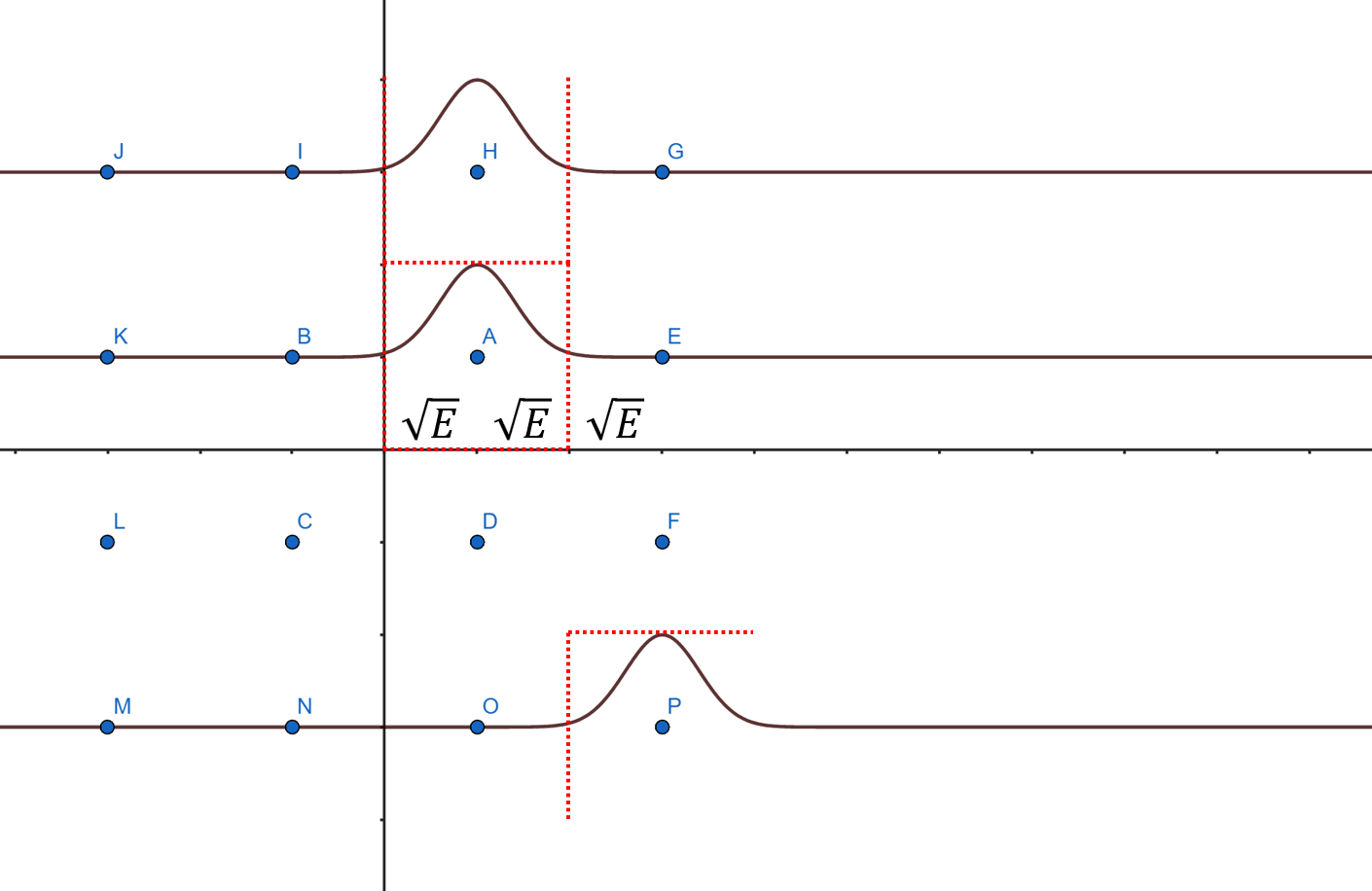
在一个16-QAM的星座图中，有三种类型的点：角点，边缘点，内点。

其中：

• 角点：J、G、P、M
• 边缘点：I、H、E、F、O、N、K、L
• 内点：A、B、C、D

本文的角点、边缘点、内点分别使用$P:(3 \sqrt{E}, -3 \sqrt{E})$、$H:(\sqrt{E}, 3 \sqrt{E})$，$A:(\sqrt{E}, \sqrt{E})$来举例。

$$S_A = \sqrt{E} + j\sqrt{E}$$

$$S_H = \sqrt{E} + 3 \sqrt{E} j$$

$$S_P = 3 \sqrt{E} – 3 \sqrt{E} j$$

其中，$\sqrt{E}$是$I$和$Q$两个维度的各自的幅度，$E$是每个维度的能量，每个符号在两个幅度上的能量之和是$2E$。

因为是16-QAM，每个符号携带的比特数为 $log_{2}(M) = 4$，因此：

$$E_b = \frac{E_s}{log_{2}(M)} = \frac{E_s}{4} $$

其中16个点的平均的符号能量$E_s$为：

$$E_s = \frac{18E \cdot 4 + 10E \cdot 8 + 2E \cdot 4}{16} = 10E$$

$$E = \frac{E_s}{10} = \frac{4E_b}{10} = \frac{2}{5} E_b$$

2. AWGN信道

在AWGN信道中，接受到的信号$r$可以表示为：

$$r = s + n$$

其中$s$是发送的信号，$n$是噪声，为复高斯随机变量，其实部$n_I$相互独立$n_Q$，每个正交的分量都服从均值为0，方差$\sigma^2 = \frac{N_0}{2}$的分布，其中整个复信号的方差为$N_0$。

3. 裁决

3.1 内点

以A点为例，需要满足在$I:(0,2 \sqrt{E})$，$Q:(0,2 \sqrt{E})$的范围内，即判定为正确的信号。

在接收端，从I分量的角度，计算A落在错误的区域$r_I<0$或$r_I>2 \sqrt{E}$的概率：

$$r = \sqrt{E} + n_I$$

$$P(r_I < 0) = P(\sqrt{E} + n_I <0) = P(n_I < – \sqrt{E}) = Q(\frac{\sqrt{E}}{\sigma})$$

$$P(r_I > 2 \sqrt{E}) = P(\sqrt{E} + n_I >2 \sqrt{E}) = P(n_I > \sqrt{E}) = Q(\frac{\sqrt{E}}{\sigma})$$

在I分量上出错的概率为：

$$Q(\frac{\sqrt{E}}{\sigma}) + Q(\frac{\sqrt{E}}{\sigma}) = 2Q(\frac{\sqrt{E}}{\sigma})$$

则落在I分量上正确的概率为$1 – 2Q(\frac{\sqrt{E}}{\sigma}) $，在这个例子中，I分量和Q分量相互独立，概率相同，同时在两个分量上正确的概率为：

$$[1 \quad – \quad 2Q(\frac{\sqrt{E}}{\sigma})]^2 $$

在两个分量上出错的概率为：

$$P_{ser} = 1 – [1 – 2Q(\frac{\sqrt{E}}{\sigma})]^2 = 4Q(\frac{\sqrt{E}}{\sigma})\quad – \quad 4Q(\frac{\sqrt{E}}{\sigma})^2$$

3.2 边缘点

以H点为例，需要满足在$I:(0,2 \sqrt{E})$，$Q:(2 \sqrt{E}, + \infty)$的范围内，即判定为正确的信号。

在接收端，从I分量的角度，计算H落在错误的区域$r_I<0$或$r_I>2 \sqrt{E}$的概率：

$$r = \sqrt{E} + n_I$$

$$P(r_I < 0) = P(\sqrt{E} + n_I <0) = P(n_I < – \sqrt{E}) = Q(\frac{\sqrt{E}}{\sigma})$$

$$P(r_I > 2 \sqrt{E}) = P(\sqrt{E} + n_I >2 \sqrt{E}) = P(n_I > \sqrt{E}) = Q(\frac{\sqrt{E}}{\sigma})$$

在I分量上出错的概率为：

$$Q(\frac{\sqrt{E}}{\sigma}) + Q(\frac{\sqrt{E}}{\sigma}) = 2Q(\frac{\sqrt{E}}{\sigma})$$

则落在I分量上正确的概率为$1 – 2Q(\frac{\sqrt{E}}{\sigma})$ 。

从Q分量的角度看，计算H落在错误的区域$r_Q< 2 \sqrt{E}$的概率：

$$r = 3 \sqrt{E} + n_Q$$

$$P(r_Q < 2 \sqrt{E}) = P(3 \sqrt{E} + n_Q < 2 \sqrt{E}) = P(n_Q < – \sqrt{E}) = Q(\frac{\sqrt{E}}{\sigma})$$

则落在Q分量上正确的概率为$1 – Q(\frac{\sqrt{E}}{\sigma})$ 。

在两个分量上正确的概率为：

$$[1 – 2Q(\frac{\sqrt{E}}{\sigma}] \cdot [1 – Q(\frac{\sqrt{E}}{\sigma})]$$

在两个分量上出错的概率为：

$$P_{ser} = [1 – 2Q(\frac{\sqrt{E}}{\sigma}] \cdot [1 – Q(\frac{\sqrt{E}}{\sigma})] = 3Q(\frac{\sqrt{E}}{\sigma})\quad – \quad 2Q(\frac{\sqrt{E}}{\sigma})^2$$

3.3 角点

以P点为例，需要满足在$I:(2 \sqrt{E}, + \infty)$，$Q:(- 2 \sqrt{E}, – \infty)$的范围内，即判定为正确的信号。

在接收端，从I分量的角度，计算P落在错误的区域$r_I<2 \sqrt{E}$的概率：

$$r = 3 \sqrt{E} + n_I$$

$$P(r_I < 2 \sqrt{E}) = P(3 \sqrt{E} + n_I <2 \sqrt{E}) = P(n_I < – \sqrt{E}) = Q(\frac{\sqrt{E}}{\sigma})$$

则落在I分量上正确的概率为$1 – Q(\frac{\sqrt{E}}{\sigma}) $，在这个例子中，I分量和Q分量相互独立，概率相同，同时在两个分量上正确的概率为：

$$[1 \quad – \quad Q(\frac{\sqrt{E}}{\sigma})]^2 $$

在两个分量上出错的概率为：

$$P_{ser} = 1 – [1 – Q(\frac{\sqrt{E}}{\sigma})]^2 = 2Q(\frac{\sqrt{E}}{\sigma})\quad – \quad Q(\frac{\sqrt{E}}{\sigma})^2$$

4. 计算BER

三类符号点出错的概率分别为：

• 内点：$P_{ser1} = 1 – [1 – 2Q(\frac{\sqrt{E}}{\sigma})]^2 = 4Q(\frac{\sqrt{E}}{\sigma})\quad – \quad 4Q(\frac{\sqrt{E}}{\sigma})^2$
• 边缘点：$P_{ser2} = [1 – 2Q(\frac{\sqrt{E}}{\sigma}] \cdot [1 – Q(\frac{\sqrt{E}}{\sigma})] = 3Q(\frac{\sqrt{E}}{\sigma})\quad – \quad 2Q(\frac{\sqrt{E}}{\sigma})^2$
• 角点：$P_{ser3} = 1 – [1 – Q(\frac{\sqrt{E}}{\sigma})]^2 = 2Q(\frac{\sqrt{E}}{\sigma})\quad – \quad Q(\frac{\sqrt{E}}{\sigma})^2$

总的符号错误概率为：

$$P_{ser} = \frac{4 \cdot P_{ser1} + 8 \cdot P_{ser2} + 4 \cdot P_{ser3}}{16} = 3 Q(\frac{\sqrt{E}}{\sigma}) – \frac{9}{4} Q(\frac{\sqrt{E}}{\sigma})^2$$

根据$\sigma = \sqrt{\frac{N_0}{2}}$：

$$P_{ser} = 3 Q(\sqrt{\frac{4}{5} \cdot \frac{E_b}{N_0}}) \quad – \quad \frac{9}{4} Q(\sqrt{\frac{4}{5} \cdot \frac{E_b}{N_0}})^2 $$

当$\frac{E_b}{N_0} \gg 1$时，可以忽略掉$Q(\sqrt{\frac{4}{5} \cdot \frac{E_b}{N_0}})^2$：

$$P_{ser} \approx 3 Q(\sqrt{\frac{4}{5} \cdot \frac{E_b}{N_0}})$$

$$BER \approx \frac{P_{ser}}{Bits \quad per \quad Symbol} = Q(\sqrt{\frac{E_s}{N_0}}) = \frac{3}{4} Q(\sqrt{\frac{4}{5} \cdot \frac{E_b}{N_0}})$$